Cauchy-Gaussian Overbound for Heavy-tailed GNSS Measurement Errors

1) What problem is this paper solving?

Context: Heavy-tailed GNSS errors (multipath, NLOS) are poorly modeled by standard Gaussian overbounds.
Core contribution: A hybrid Cauchy-Gaussian overbound that uses Cauchy for the sharp core and Gaussian for the tails.
Achieved goal: Tighter, integrity-preserving error bounds for both symmetric and asymmetric heavy-tailed distributions.

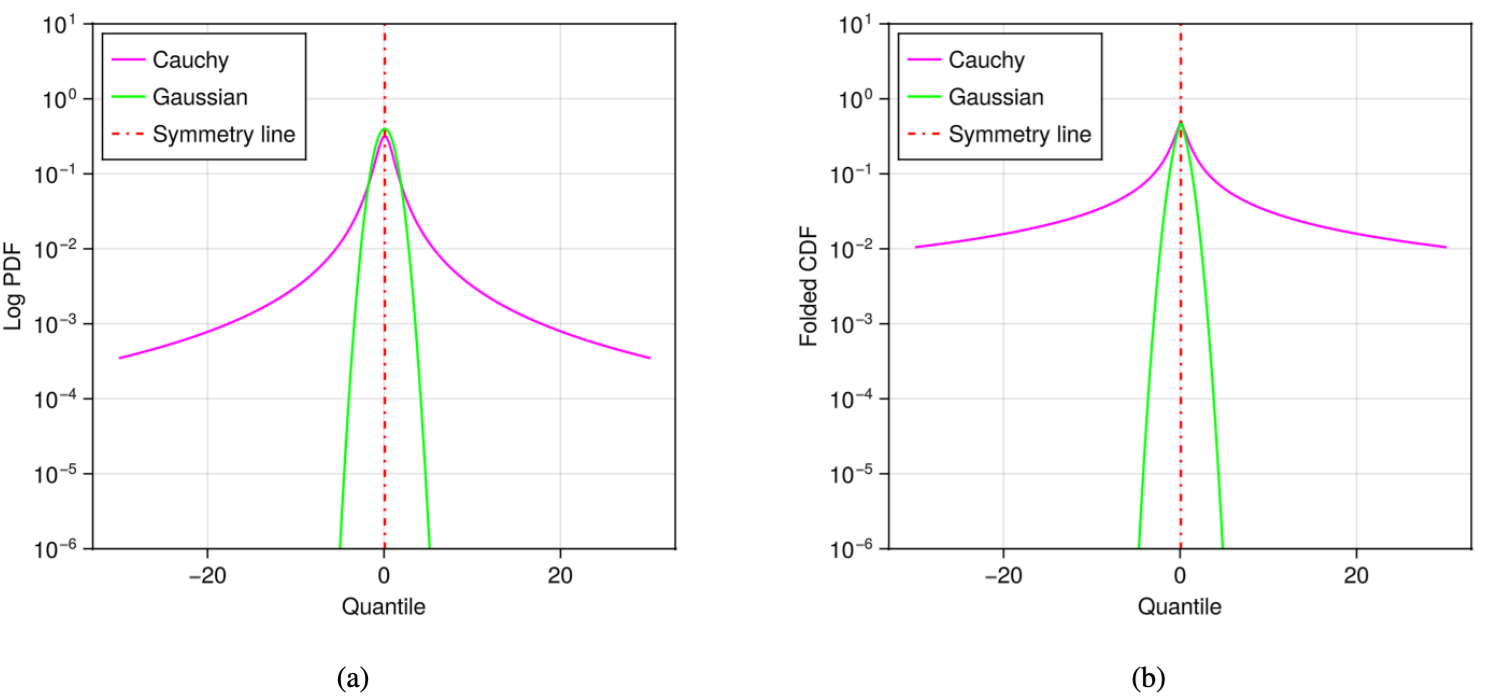Comparison between the standard Cauchy and Gaussian distributions, through (a) PDF and (b) folded CDF on a logarithmic scale.

2) Why is this paper important?

What changed: Urban navigation demands high integrity, but Gaussian bounds are too loose (conservative) for heavy tails.
Problem created: Excessive conservatism leads to huge Protection Levels (PL), making the system unavailable.
Why current solutions fail: Gaussian bounds over-inflate sigma to cover tails.

3) How does this paper solve it?

Contribution 1: Leverages the Cauchy distribution’s sharp peak to tightly bound the error core.
Contribution 2: Transits tangentially to a Gaussian distribution to safely bound the tails.
Key result: Reduced Vertical Protection Level (VPL) by 15% (symmetric errors) and 21–47% (asymmetric errors) vs. baselines.

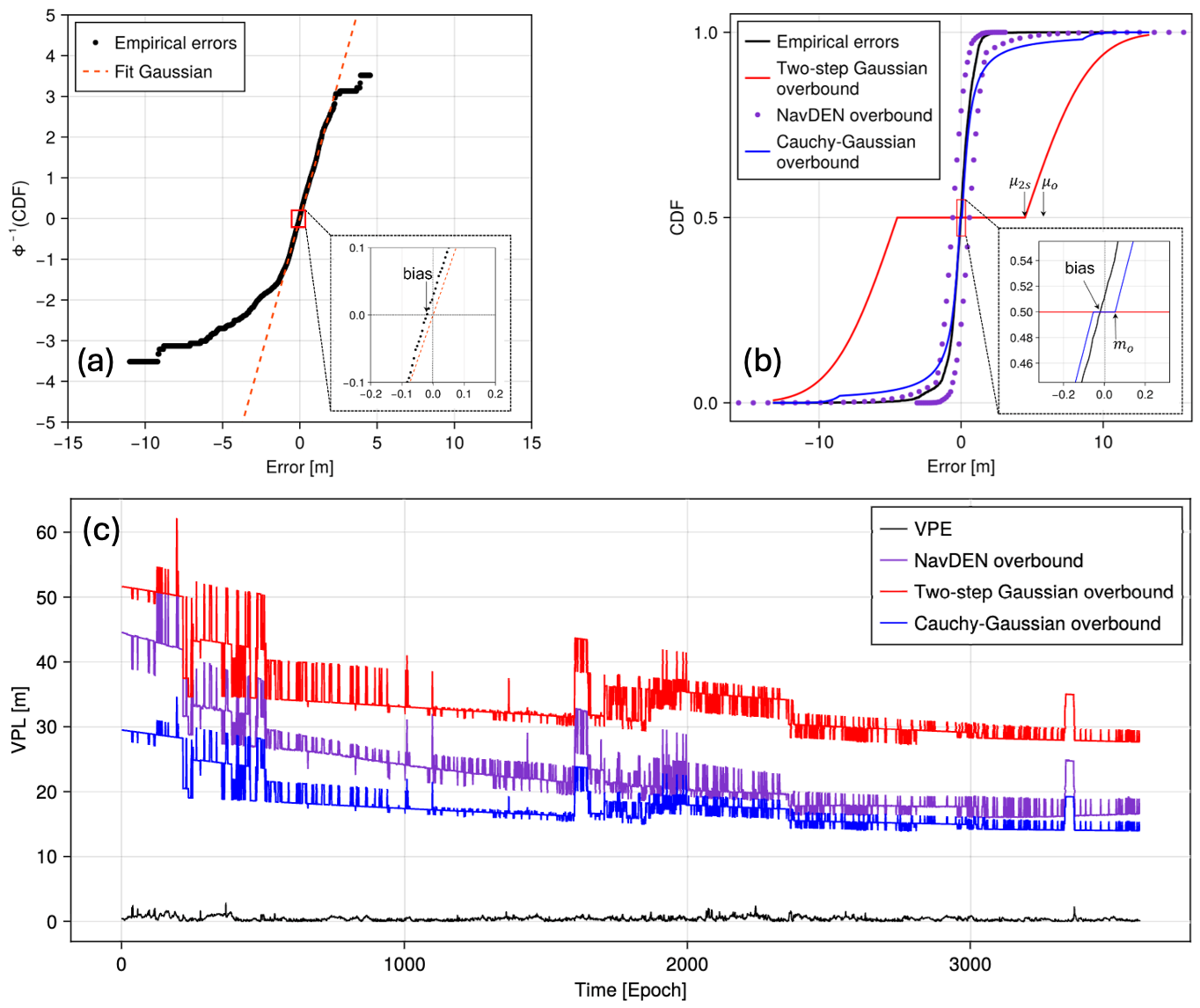(a) Quantile-scale CDF showing empirical DGNSS error in urban areas are heavy-tailed; (b) CDF of the two-step Gaussian overbound, NavDEN overbound, and the Cauchy-Gaussian overbound; (c) VPL produced by the three overbounds at PHMI of 10^-9.

🎯 Takeaway: Combining Cauchy sharpness with Gaussian tails creates a tighter, safer bound for urban GNSS integrity.

@article{li2026cauchy,
  author = {Li, Zhengdao and Yan, Penggao and Wen, Weisong and Hsu, Li-Ta},
  title = {Cauchy-Gaussian Overbound for Heavy-tailed GNSS Measurement Errors},
  journal = {NAVIGATION: Journal of the Institute of Navigation},
  year = {2026}
}