Bounding the Heavy-tailed DGNSS Error by Leveraging Membership Weights Analysis of Gaussian Mixture Model

In this study, we present a novel approach to overbounding heavy-tailed error distributions by leveraging the Gaussian mixture model. Specifically, we employ the bimodal Gaussian mixture model (BGMM) and utilize the expectation maximization (EM) algorithm [14] to accurately fit the error distribution. The membership weights of the BGMM are analyzed, and the membership weight of the tail component is proved to be a convex function of the error. Then, we introduce a partitioning strategy based on the convex property of the tail component’s membership weight, which effectively divides the BGMM into the core and tail regions. In each region, one of the Gaussian components of the BGMM holds a dominant position, and a CDF overbound is constructed based on the inflation and shifting of the dominant Gaussian component. The proposed overbound is proved to be an unimodal and symmetric distribution, which indicates that its overbound property can be preserved through convolution.

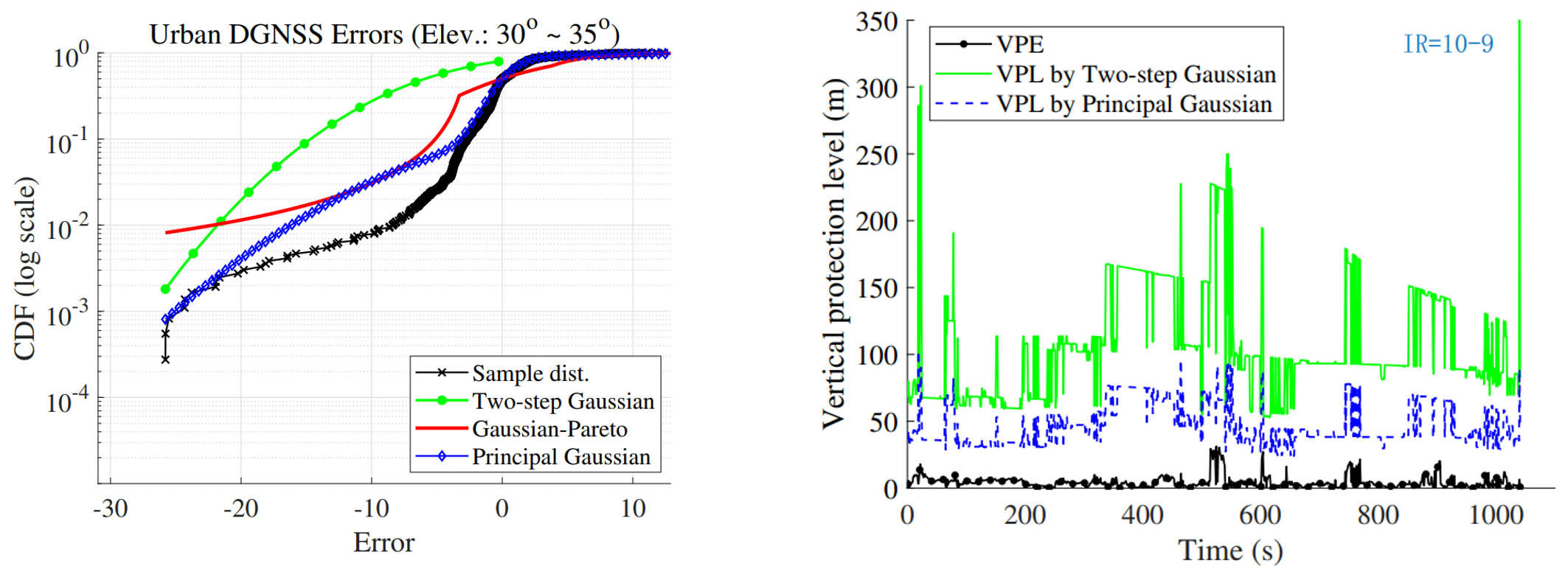(a) The CDF (in logarithm scale) of the proposed method (Principal Gaussian overbound), the two-step Gaussian overbound, Gaussian-Pareto overbound for Urban DGNSS errors (heavy-tailed distribution); (b) The protection level of LS solution based on the proposed method (Principal Gaussian overbound) and the two-step Gaussian overbound when integrity risk is set as 10^-9.

Recommended citation: Yan, P., Zhong, Y., & Hsu, L. T. (2024, April). "Bounding the Heavy-Tailed Pseudorange Error by Leveraging Membership Weights Analysis of Gaussian Mixture Model". In Proceedings of the ION 2024 Pacific PNT Meeting (pp. 541-555).
Download Paper | Download Slides